Оглавление электронного пособия

Справочник


Уравнением с одним неизвестным (аргументом) называется равенство значений двух функций f1(x) = f2(x) одной переменной, рассматриваемых в их общей области определения. Решить уравнение - значит найти все значения переменной, при которых указанное равенство имеет место.

Неравенством с одним неизвестным (аргументом) называется выражение вида f1(x) > f2(x), связывающее две функции одной переменной, рассматриваемые в их общей области определения. Решить неравенство - значит найти все значения переменной, при которых указанное соотношение имеет место.

В выражении

a b = c, a > 0,

c или a b - степень,
a - основание степени,
b - показатель степени.

Функция f(x) называется монотонной, если для любых значений переменной x1 и x2 из ее области определения, связанных соотношением x1 < x2, разность f1(x) - f2(x) всегда имеет один и тот же знак. Если этот знак " +" - функция убывает, если этот знак "-" - функция возрастает.

Теорема о корне уравнения

Теорема.

Если p - любое из значений, принимаемых монотонной функцией f(x) на некотором промежутке, то уравнение f(x) = p имеет единственный корень в этом промежутке.

Доказательство.

Рассмотрим уравнение f(x) = p, где функция f(x) возрастает на рассматриваемом промежутке. По условию теоремы в промежутке существует такое число b, что f(b) = p. Покажем, что b - единственный корень уравнения. Допустим, что существует число c ≠ b такое, что f(с) = p , тогда с < b или с > b. В первом случае f(c) < f(b), во втором случае f(с) > f(b), что противоречит равенству f(с) = f(b)= p. Следовательно, уравнение f(x) = р имеет в рассматриваемом промежутке единственный корень b.

Действия со степенями

(a > 0, b > 0, m и n - любые действительные числа).

Основное логарифмическое тождество

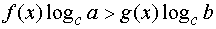
(a > 0, a ≠ 1, m > 0)
следует из определения логарифма: действительное число b называется логарифмом числа m по основанию a, если a b = m.

Обозначение логарифма:

Прологарифмировать данное выражение - значит выразить его логарифм через логарифмы компонентов.

Основные правила логарифмирования:

При a > 0, a ≠ 1, b > 0, c > 0 и любом действительном m верны следующие равенства:

Вынесение общего множителя за скобки рассмотрим на примерах.

Пример 1.

a 2x+4 + 2a 3x+2 = a 2x+2(a 2x+4–2x–2 + 2a 3x+2–2x–2) = a 2x+2(a 2+ 2a x).

Пример 2.

a 5b – a 3b 2 = a 3b(a 5–3– b 2–1) = a 3b(a 2– b).

В скобках выполняется вычитание показателей степеней с одинаковым основанием, так как при вынесении общего множителя за скобки выполняется деление на него каждого слагаемого.

Уравнение называется однородным относительно функций f1(x) и f2(x), если оно удовлетворяет следующим условиям:

Например, уравнения

однородны относительно функций f1(x) = cosx и f2(x) = sinx, а уравнение

однородно относительно функций f1(x) = a f(x) и f2(x) = b f(x).

Два уравнения (неравенства) называются равносильными или эквивалентными, если каждое решение первого из них является решением второго и, наоборот, каждое решение второго является решением первого или оба уравнения (неравенства) не имеют решений.

Неравенство вида ax 2+ bx + c > 0 (<, ≥, ≤) называется квадратным алгебраическим неравенством. Для его решения можно использовать метод интервалов или параболу - график функции y = ax 2 + bx + c.

Пример.

Решить неравенство x 2- 5x + 6 > 0.

Решение 1 (методом интервалов).

Выполним разложение многочлена на множители: y = x 2- 5x + 6 = (x - 2)(x - 3).Изобразим на оси Ox точки перемены знаков множителей: x1=2 и x2=3. Расставим знаки многочлена.
Решениями неравенства будут значения x<2 и x>3.

Решение 2 (с использованием графика параболы).

Точки пересечения параболы y = x 2- 5x + 6 с осью Ox соответствуют значениям x1=2 и x2=3. Ветви параболы направлены вверх, так как коэффициент при x 2 положителен.
Решениями неравенства y >0 являются значения x<2 и x>3.